Pathfinding in Classic CRPGs
(TLDR? There is a video at the bottom of this post.)
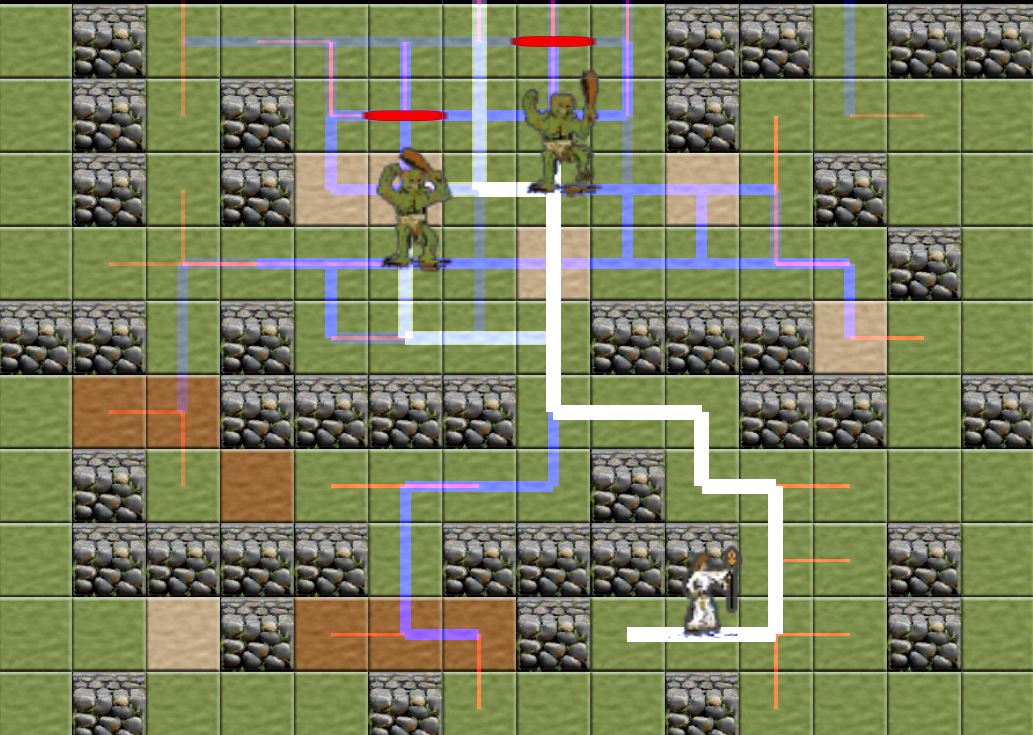
Classic CRPG pathfinding left a lot to be desired. And while we want to recreate the feel of those old CRPGs, nobody wants overly-dumb baddies. So, it was past time to finally upgrade the NPC pathfinding AI. (Before this, the system had the baddies move toward the player.) You know, something like this:
if (player.x < monster.x) monster.x--;So, this project finally gave me a good reason to implement A* pathfinding.
NavMesh?
In most Unity projects, I'd simply recommend using the NavMesh system. It is a ridiculously powerful tool that has come in handy for me during a variety of past projects including everything from mobile arcade games to business apps in VR. But it seemed like overkill for a tile-based CRPG. If you want to know more about Unity's NavMesh, this guy's tutorial is a great intro.
The A * Algorithm
So.. if I wasn't going to use Unity's NavMesh, everybody knows that the famous A* algorithm (pronounced "A STAR") is the best place to start for path-finding, but I had never actually implemented it from scratch. A quick Google search landed me on this guy's C# implementation. He references this other guy. A quick scan of those two and a read of the Wikipedia article to refresh myself on how it is supposed to work, I started coding and had the basic algorithm working in half an hour. It really is that straight forward. I can't believe it took me this long to give it a try.
Of course there is a lot of nuance that goes into all of this after the basic implementation. For example:
- Are all baddies really that smart (for suspension of disbelief or gameplay reasons)?
- What are the limits of how long a path can be for performance reasons?
- How often are paths recalculated (again, for performance)?
- How do you account for dynamic objects?
- Are the various terrain costs appropriately balanced?
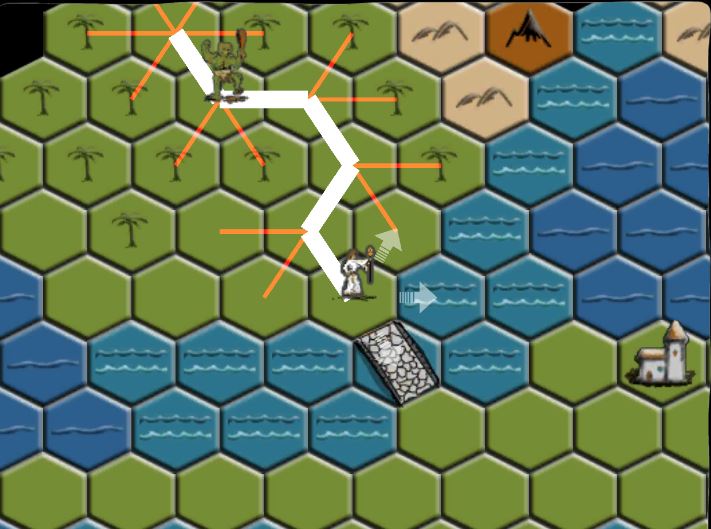
But the big question before I started was the question of how well the A* algorithm would lend itself to the hex-grid. And as I should have expected, the answer is "beautifully... it handles hex-grids beautifully".
Basically, the algorithm tracks two lists, the "open list" and the "closed list". (The open list is just a list of all the cells we have noted that we want to do some calculations on and the closed list is all the cells we have already done some calculations on.)
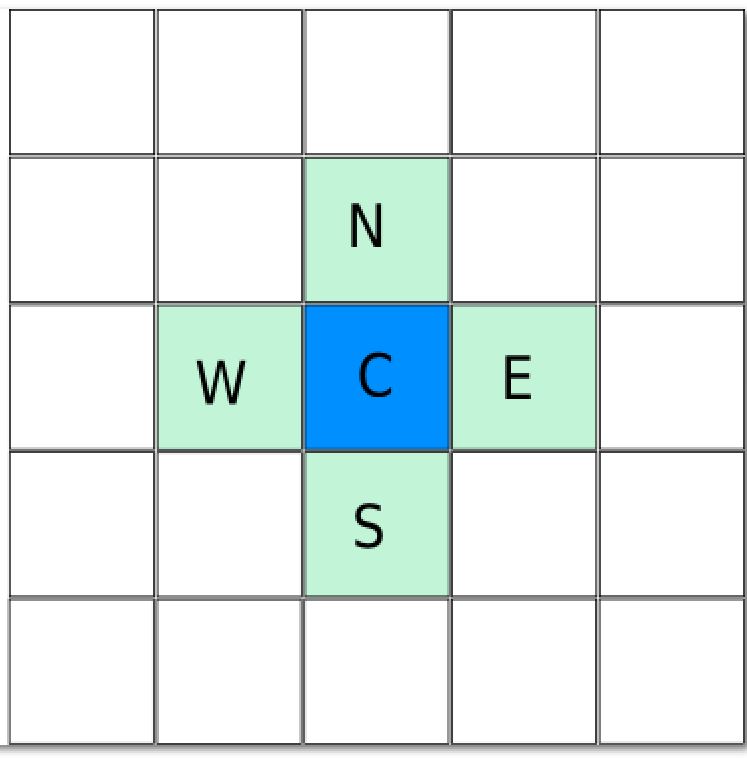
Then we loop through the cells in the open list. And .... the first step in that loop is to add the current cell's neighbors into to the open list. In a square-grid you have four neighbors. In a hex-grid you have six. (See below)
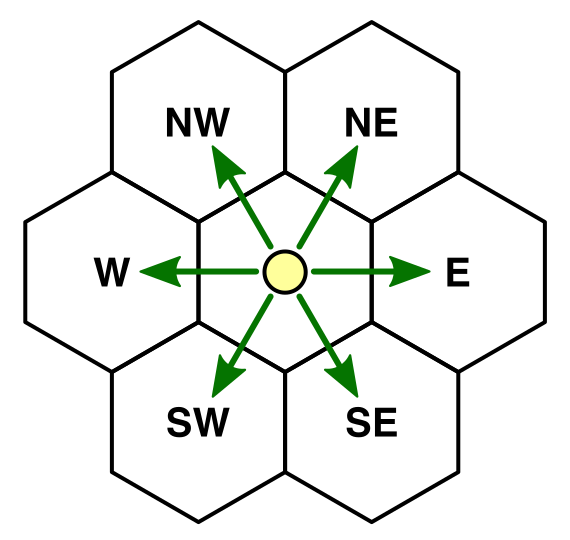
So for a hex-grid, we only have to place two more entries into the open list than we would if it was a square grid!
There is one small catch... What are the actual coordinates of those neighbors in the Unity Tilemap implementation?
Well, it depends on what row you are in.
- If the y-value of the cell is even, then the NE and SE cells have the same x-value.
- If the y-value of the cell is odd, then the NW and SW cells have the same x-value.
Lets see some code!
So my code for adding neighbors basically looks like this:
static List<Vector3Int> AddNeighbors(bool p_isHex, Vector3Int p_pos)
{
if (!p_isHex)
{
Vector3Int[] allNeighbors =
{
new Vector3Int(p_pos.x + 1, p_pos.y, 0),
new Vector3Int(p_pos.x - 1, p_pos.y, 0),
new Vector3Int(p_pos.x , p_pos.y + 1, 0),
new Vector3Int(p_pos.x , p_pos.y - 1, 0)
};
return new List<Vector3Int>(allNeighbors);
}
else
{
if (p_pos.y % 2 == 0)
{
//if y is even, we need to add the ne (x-1)(y+1)
//if y is even, we need to add the se (x-1)(y-1)
Vector3Int[] evenHexNeighbors =
{
new Vector3Int(p_pos.x + 1, p_pos.y, 0),
new Vector3Int(p_pos.x - 1, p_pos.y, 0),
new Vector3Int(p_pos.x , p_pos.y + 1, 0),
new Vector3Int(p_pos.x , p_pos.y - 1, 0),
new Vector3Int(p_pos.x - 1, p_pos.y + 1, 0),
new Vector3Int(p_pos.x - 1, p_pos.y - 1, 0)
};
return new List<Vector3Int>(evenHexNeighbors);
}
else
{
//if y is odd, we need to add the nw (x+1)(y+1)
//if y is odd, we need to add the sw (x+1)(y-1)
Vector3Int[] oddHexNeighbors =
{
new Vector3Int(p_pos.x + 1, p_pos.y, 0),
new Vector3Int(p_pos.x - 1, p_pos.y, 0),
new Vector3Int(p_pos.x , p_pos.y + 1, 0),
new Vector3Int(p_pos.x , p_pos.y - 1, 0),
new Vector3Int(p_pos.x + 1, p_pos.y + 1, 0),
new Vector3Int(p_pos.x + 1, p_pos.y - 1, 0)
};
return new List<Vector3Int>(oddHexNeighbors);
}
}
}See it in Action
Okay, now add some debug lines to draw and things start to look great!
(Note that the Debug.DrawLine wasn't working for me, so I started with this DebugLine and modified it for my purposes.) You can find my updated DebugLine code at the bottom of this post.
Putting it all together in motion is where it starts to get fun. Here is a short video that makes it hard to believe it really was that easy!
Until next time, happy coding!
-John