Chess is a game that requires both deep and broad calculation. A chess grand-master can quickly see twenty moves ahead (depth) and evaluate the overall position of a chess board (breadth) in a blink of an eye.

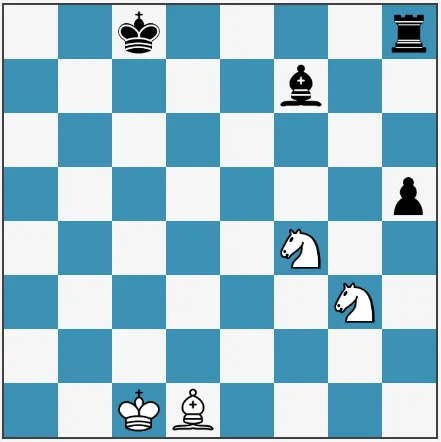
One basic step in evaluating a board position is to calculate the number of threats on a piece. A piece that is threatened by several opponent pieces and not protected by an equal number of defending pieces is a potential target for attack. As an example, in the picture below the white benefits from capturing the h5 pawn.
A person (and even a game engine) cannot analyze every possible move to the end, but instead uses various techniques to quickly evaluate a position and identify promising candidate moves. This techniques are usually known as pruning.
A while ago, I was thinking about methods that a chess engine uses to analyze a chess position, so that I can mimic and improve my chess skills. I thought that keeping track of the overall number of threats on a square during a match might be a good approach, as interesting maneuvers tend to happen to pieces on squares which is dominated by the opposite color (the number of threats from black minus the number of threats from white). In the image below, a positive(+) numbers shows that a square is dominated by white and a negative(-) numbers shows that a square is dominated by black. The number itself shows the domination strength. In the chess board before the black pawn on h5 was in a square that was dominated by white (three white pieces against 2 black pieces):
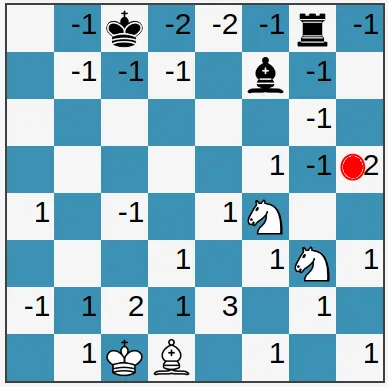
As I was thinking about this and day-dreaming about how to update the threat value array after each move, a game-related question came to mind:
How can we efficiently and quickly update this threat number table without recalculating everything from scratch?
While doodling my ideas on an 8×8 table, I forgot about the chess pieces and ended up with an 8×8 board filled with numbers, similar to a Sudoku puzzle* . I had a puzzle to solve, but it was not about adding numbers but adding pieces to the board to figure out the original chess position. It was indeed a difficult riddle. I attempted to solve a few of these puzzles by just having the numbers on the board, but found them to be very difficult or may end up with several solutions. What if we knew the exact pieces on the board but not their positions? This seems to be easier to solve and this is how the idea of Chedoku emerged in mind.
You can try it at
I hope you will consider trying my game and solving some Sudoku puzzles. I think you will love it!
In the next posts I will talk about other different variants of Chedoku.
* Several people later told me that the game is more like Minesweeper, where you search for hidden mines based on numbers revealing how many mines are next to a given square.
