Hello World
First game post! Here we go! Why the hell am I here?!
Basically, I decided I wanted to start doing a dev diary as I work on my game, and IndieDB seemed like a logical enough place to do that, so here I am. I've already been working on this project for a couple weeks, so I've had ample time to implement some basic features. Therefore, I'll be spending the first few posts just playing catch-up, and this is the first one: how do we deal with the third-person perspective shooting dilemma?
The Dilemma
Look, if I'm shooting in a game, I expect my bullet to go where my crosshair is pointing. Maybe in your game, the goal is to piss players off so that when they shoot the bullet trace picks a random pixel on the screen, and if so, more power to you m8. But in most games, that's how it is. Now, in a first-person game, that's not a problem if you center the crosshair and shoot a line trace straight out of the camera; it goes right where you want it to basically every time. Great!
Problem is in third-person games... you can't shoot out of center screen all the time. If my character is off to the left, say, behind a wall, but my crosshair is pointing at a player on the other side, that's a problem. I'd be able to hit that player while remaining perfectly protected behind a wall! Now, the way I've seen most indie devs resolve this is quite straightforward: let's calculate the position where the center screen line trace hits and then spawn our projectile on a trajectory from the muzzle of the gun to that impact point. That way, even if our crosshair is on a player, if we're behind a wall we won't hit them. It would look like this:
Perhaps it's a bit hard to see, but notice how my crosshair is aiming at the ground behind the wall, and the trace (the green line) from the muzzle is going to that point, but I'm actually hitting the wall. That's good! We don't want to be able to shoot around walls!
BUT. It's not the whole story, is it? Because imagine if that wall I'm hitting in the image above was a player. And then you look at your killcam and you're like... "dude, he literally didn't even hit me?!" And your friend calls you a whiner, of course, but seriously! It wasn't your fault! Clearly that guy's crosshair is aiming NEXT to you, not ON you. This obviously does not make for a good gaming experience in PvP AT ALL.
Luckily, there is a solution to this that is reasonably simple...
Solution
I should emphasize, of course, that this is one solution that I came up with, not the solution. In addition to different games having different requirements, there are surely a thousand ways of dealing with this. This is the one that I chose based on its simplicity and ease of implementation in UE4.
So, let's think about the cases we want to avoid. There are two big ones. 1) We don't want the player to hit an enemy while the player is hidden from their sight. 2) We don't want the player to hit an enemy when the crosshair is not on them.
The solution to 1) is to shoot from the muzzle, as explained above. A solution to 2) is to simply fire two separate line traces, one from center screen and one from the muzzle, and to compare the hit results; if center screen trace did NOT hit a player, but muzzle trace DID hit a player, we have a problem! Here's some psuedo code for my implementation:
IF (CenterScreen_CharacterTrace Hit) -> Spawn projectile with collision from muzzle to impact point
ELSE IF (CenterScreen_ObjectTrace Hit OR Missed) AND IF (Muzzle_CharacterTrace Hit) -> Spawn one projectile WITH collision from center screen, and another projectile WITHOUT collision from muzzle to impact point
ELSE IF (CenterScreen_ObjectTrace Hit) AND IF (Muzzle_ObjectTrace Hit) -> Spawn projectile with collision from muzzle to impact point
ELSE IF (CenterScreen_Object Trace Missed) AND IF (Muzzle_ObjectTrace Hit OR Missed) -> Spawn projectile with collision from muzzle to end of trace
... And you can check out the results in the video below! (read on for an explanation of the colored line traces):
TPS Perspective Tracing - Indie DB
Let's break down each of those lines of pseudo code and why we need them. I'll illustrate the results with some screenshots from my prototype as well. Let's start with line 1...
IF (CenterScreen_CharacterTrace Hit) -> Spawn projectile with collision from muzzle to impact point
Very straight-forward. If the center screen character trace hits, we definitely want to spawn a projectile with collision no matter what, because we expect to hit that player (barring a wall being in the way!)
Note also that I said "character trace" specifically. In my implementation, I chose to use two separate trace channels rather than cast the actor I hit, for the simple reasons that A) it turned out to be more efficient than casting and B) I'm using those traces for other features anyway.
Ok, on to line 2...
ELSE IF (CenterScreen_ObjectTrace Hit OR Missed) AND IF (Muzzle_CharacterTrace Hit) -> Spawn one projectile WITH collision from center screen, and another projectile WITHOUT collision from muzzle to impact point
This is the really important one. Check out the red trace in the screenshot above. That's my muzzle trace; as you can see, my crosshair isn't on the mesh's head, but if I shot from the muzzle I'd hit her smack dab in the middle! Instead of doing that, I spawn two projectiles: One invisible projectile from center screen with collision (which you can see hitting the wall behind the mesh) and one cosmetic projectile with NO collision from the muzzle.
It is worth noting that technically the cosmetic projectile does pass through the mesh's head, but for my use case this is a non-problem entirely. The projectiles are too fast to notice (they'd be even less noticeable online), this is not a common case in-game, and it is a 10000% MUCH better experience than a player wondering why they died to someone who wasn't aiming at them (obviously we still need to worry about lag, but... well, we'll save that for another day <3)
On to line 3...
ELSE IF (CenterScreen_ObjectTrace Hit) AND IF (Muzzle_ObjectTrace Hit) -> Spawn projectile with collision from muzzle to impact point
Huh, that picture's familiar... yep, if the center screen and muzzle traces both hit non-player objects, we just spawn a projectile as usual from the muzzle! I will also be adding an indicator icon letting the player know they are hitting a wall, but the important thing is that they definitely hit the wall.
Finally, line 4 is a rarer case where the center screen traces don't hit anything, meaning the player is shooting at the sky or something...
ELSE IF (CenterScreen_Object Trace Missed) AND IF (Muzzle_ObjectTrace Hit OR Missed) -> Spawn projectile with collision from muzzle to end of trace
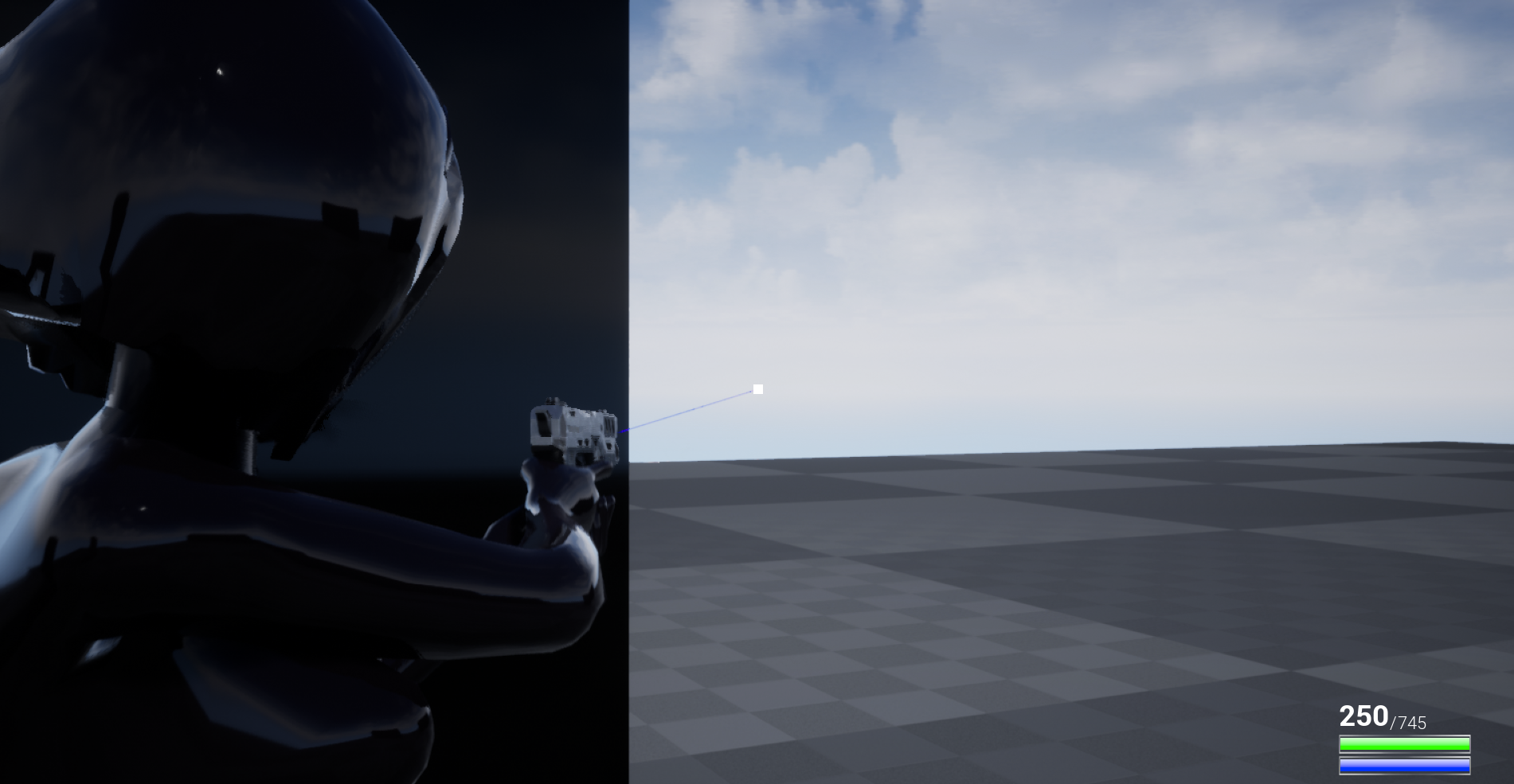
I have a blue line trace for that as shown below:
For some reason, I feel like I should also mention these colored line traces are for debugging only... they won't be in the actual game. In case you thought that. Sorry to disappoint :P
Conclusion
Well, that about does it! A fairly simple solution that I haven't seen suggested anywhere, so I thought I would share it since it's one of the first things I set about implementing in my game. Of course, we shouldn't be naive in thinking we're all done here; there are some other edge cases to be handled as well! Here's a lovely example of just that...
I used an orange trace for this because I despise orange, by the way. Just thought you all should know that.
In any case, yes, as you can see my crosshair is on the mesh's arm, but I am in fact IN FRONT of the mesh. If we left the code as it was, it would say, ok, center screen hit a player, so spawn a projectile from muzzle to the impact point... meaning, in case you haven't already figured it out, my projectile would go BACKWARDS and then I would get mocking Steam reviews telling me all about how people can shoot BEHIND THEMSELVES.
Very bad. So, we detect this case by doing some vector math (Hint: vector between the muzzle and the center screen impact, rotation of the muzzle, and dot product) and make sure we shoot from the muzzle to the end of the MUZZLE trace instead. And all is well in the world once again :)
Thanks for reading, and hope you learned something! I can't wait to share more of this game, especially once the pretty 3D models and such start coming along. But for now, implementation, implementation!
- Flash <3






This comment is currently awaiting admin approval, join now to view.