Although there's only so much information ASCII alone can hold without color or a supporting interface, it's still worth it for morgue files to include a map of the area around the player at the end of the run for added context. For wins generally not so much, but such maps can definitely be useful for determining the tactical circumstances behind a loss. (That said, some wins while on the verge of death are only even made cooler with a final map showing a horde of hostiles on one's tail!)
Last time I covered the general organization of Cogmind's Scoresheet 2.0, but wanted to get into more detail with maps in particular since there's a lot to say/show.
Other Roguelikes
Three out of four of the roguelikes I surveyed earlier for their morgue file content include an ASCII map within it.
ADOM's morgue file is topped by a console screenshot taken at the end of the run, so naturally includes the surrounding area. Here I've taken a few maps from different morgue files to give you an idea.

ADOM morgue file map samples.
Unlike the others, DoomRL (DRL) reveals the entire map, regardless of whether it was explored or not:

DoomRL (DRM) morgue file map samples.
And DCSS morgue file maps show a relatively small area (interesting since it also has the largest maps of these three roguelikes), but are also the only ones to use Unicode characters--the other two are pure ASCII.

DCSS morgue file map samples.
Cogmind Style
For Cogmind I decided to go with pure ASCII. One of the big limitations of exporting a text map this way is that it can't show Cogmind's machines properly. These are drawn with CP437 (extended ASCII), but I want the entire scoresheet to be widely compatible and not require any special encoding, which means we have to forgo Unicode. (Not to mention non-ASCII characters can look especially weird depending on the font, and because they're narrow rather than square like in game, machines' appearance is otherwise significantly distorted anyway.)

An example of what happens when character encoding can't be interpreted correctly and requires manual/reader adjustment (not ideal!).
Well in most cases the type of machine is not terribly important, so I decided to draw all of them using a character not used elsewhere: the double quote. Interactive machines are certainly important, so their interactive piece is still represented by the appropriate capital letter, making it possible to distinguish that particular machine block from the rest. This is looking better:

The initial concept for Cogmind's scoresheet ASCII map style.
Here I've also added a border around the map view, which comes in handy when near map borders, or when the known map doesn't fill the available area. I left empty buffer columns to the left and right of the map, but not the top and bottom; this is because as a text file it will generally be viewed using a non-square/tall font, so the spacing looks more even this way.
In terms of area, Cogmind shows all known terrain and objects within a 50x50 area (the smallest), where areas outside FOV are output as whatever the player remembers to be there.
You'll also notice that debris is completely removed (anything that would just be noise and interfere with interpreting the map shouldn't be there, especially since there's no cellwise brightness we can use to emphasize/de-emphasize various elements). This was actually kinda hard to do for previously seen areas and required a bit of a hack to retroactively "erase" debris ASCII without misinterpreting actual item knowledge.
At this point I started testing out various different map styles. Do we want to be able to distinguish between FOV and non-FOV areas? How should unexplored areas be represented? I did tests of each to compare... (see legends)

ASCII map style concept 2.

ASCII map style concept 3.

ASCII map style concept 4.

ASCII map style concept 5.
I decided the last one is best, as it's not too meaningful to distinguish FOV vs. non-FOV areas, especally when doing so has the drawback of making the map harder to read. Much more important are the objects present, specifically the letters (robots).
On that note, I wonder if it would end up being useful to have a description of major features on the map, such as the names of meaningful robots and parts that can't necessarily be gleaned from the ASCII map alone (like technically an 's' could represent a weak robot, or a very powerful one, although cases like this aren't too prevalent, and some can be determined through other context clues).
Anyway, I worked out some kinks in the content and did some more tests. If you've played Beta 8, you'll probably recognize this place :)

Cogmind ASCII map style in Exiles lab.
Here's what the caves look like in this style:

Cogmind ASCII map style in caves.
Then I went back and added a way to see the edges of the map (as with the advanced.cfg showMapBorders setting):

ASCII map style concept 1 with inner/map border.
But after all that work realized such a feature is pointless if going with a style that marks unknown cells, which reveals the map border naturally xD

ASCII map style concept 5 without explicit inner/map border.
Duh.
Samples
ASCII maps aren't even in the public release yet, but patrons have been trying out the system in recent weeks and I'm already really liking the results as I examine scoresheets. Here are some samples from real runs...

The classic Assembled and Demolishers in the Mines. Killed by a grenade.
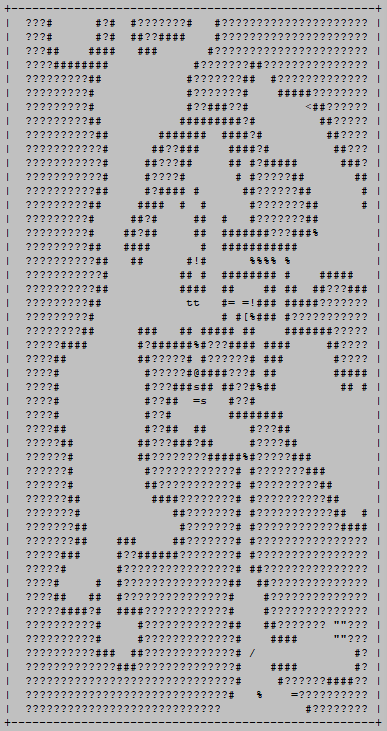
Another sample Mines death, albeit to more mundane causes (a Swarmer patrol).

Getting dogpiled in a late-game branch. Mistakes were made.

Beta 9 makes Garrisons very inviting. But this doesn't make them any less dangerous!

Clearly there was some serious exploding going on here.
Fun
Not long after Cogmind's map could be output in ASCII form for the scoresheet, I realized I could do something with them that I'd wanted to do for a while but didn't have the means.
REXPaint has the ability to import text files (via the -txt2xp switch), so I could take map views from Cogmind and doctor them in the editor! I do a lot of map editing in REXPaint, but it's mainly for prefabs, and of course it's in the REXPaint->Cogmind direction. With the direction reversed, it's easy to dynamically play with other font styles and colors using the editor's features.
For fun I took a sample map and colored it in the original C64 font:
C64 Cogmind

The original ASCII text as it appeared in the scoresheet.
And a screenshot of the area in game.
I don't have any practical applications for this right now, though I recall in Cogmind's early years I did consider using something like this for testing purposes and/or to compile marketing materials.
Anyway, it's a thing, but the main point is having maps improves yet another facet of scoresheets :D
This is the second article in a four-part Building the Ultimate Roguelike Morgue File series.



